22.括号生成

题目：Leetcode 22.括号生成 （一刷） （中等）

解题思路：

括号对称组合等问题，一般可以使用动态规划或DFS或BFS。

一、动态规划

因为题目给出了n，要求满足n对有效括号的组合。所以我们可以以()为整体进行动态添加，那么问题来了，我们该如何添加？

举个简单的例子：

假设 n = 2

当 i = 1（i表示存在有效括号的对数），此时只有一种可能();

当 i = 2时，我们有3中添加括号对的位置，分别为左，中，右,为了避免有效括号对的组合中存在重复对。因此我们只需要
在左和右中任选一个位置。在我的代码中，我选择了中和右两个位置。

注：

三种位置分别为：(右)(中), ((中中)),(中)(右)

---

选定了思路之后，我们接下来就可以动态规划的步骤一步步实现：

① 定义状态:dp[i] 表示i个括号对组合列表

② 状态转移方程：状态转移方程: 分为两个部分,形如’(‘+dp[j]+’)’+dp[i-j-1]，这样就实现了在中间和右边添加。

注意到 j +(i-j-1) = i-1，因为最终的组合括号对是上一个i个括号对的组合在加上()。

③ 初始化:dp = dp = [[‘’,] for _ in range(n+1)]，dp[1] = [‘()’,]，空间复杂度可能有点高，需要优化

④ 选取结果：选取dp[-1],也就是n对组合的列表

代码：

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        # 动态规划
        # 定义状态:dp[i] 表示i个括号组合列表
        # 状态转移方程: 分为两个部分,形成'('+dp[j]+')'+dp[i-j-1]。
        # 初始化:dp = dp = [['',] for _ in range(n+1)]，dp[1] = ['()',]
        # 选取结果dp[-1]
        if n == 0:
            return ['']
        dp = [['',] for _ in range(n+1)]
        dp[1] = ['()',]
        for i in range(2,n+1):
		    # 从2开始
            cur = []
            for j in range(i):
			    # 分出左右两个部分
                left = dp[j]
                right = dp[i-j-1]
				# 进行排列组合
                for m in left:
                    for n in right:
                        cur.append('('+m+')'+n)
            dp[i] = cur
        return dp[-1]

注：分析代码，我们可以看出后一次的组合的括号对数会依赖于前一次的组合括号对数。这就是动态规划的特征之一，得到了全局最优解，将大的问题拆分成小的问题进行解决

---

二、深度优先遍历

深度优先遍历主要有两种方式：

① 利用系统栈的回溯递归

② 利用栈来实现DFS

截取一位大佬的DFS过程图：

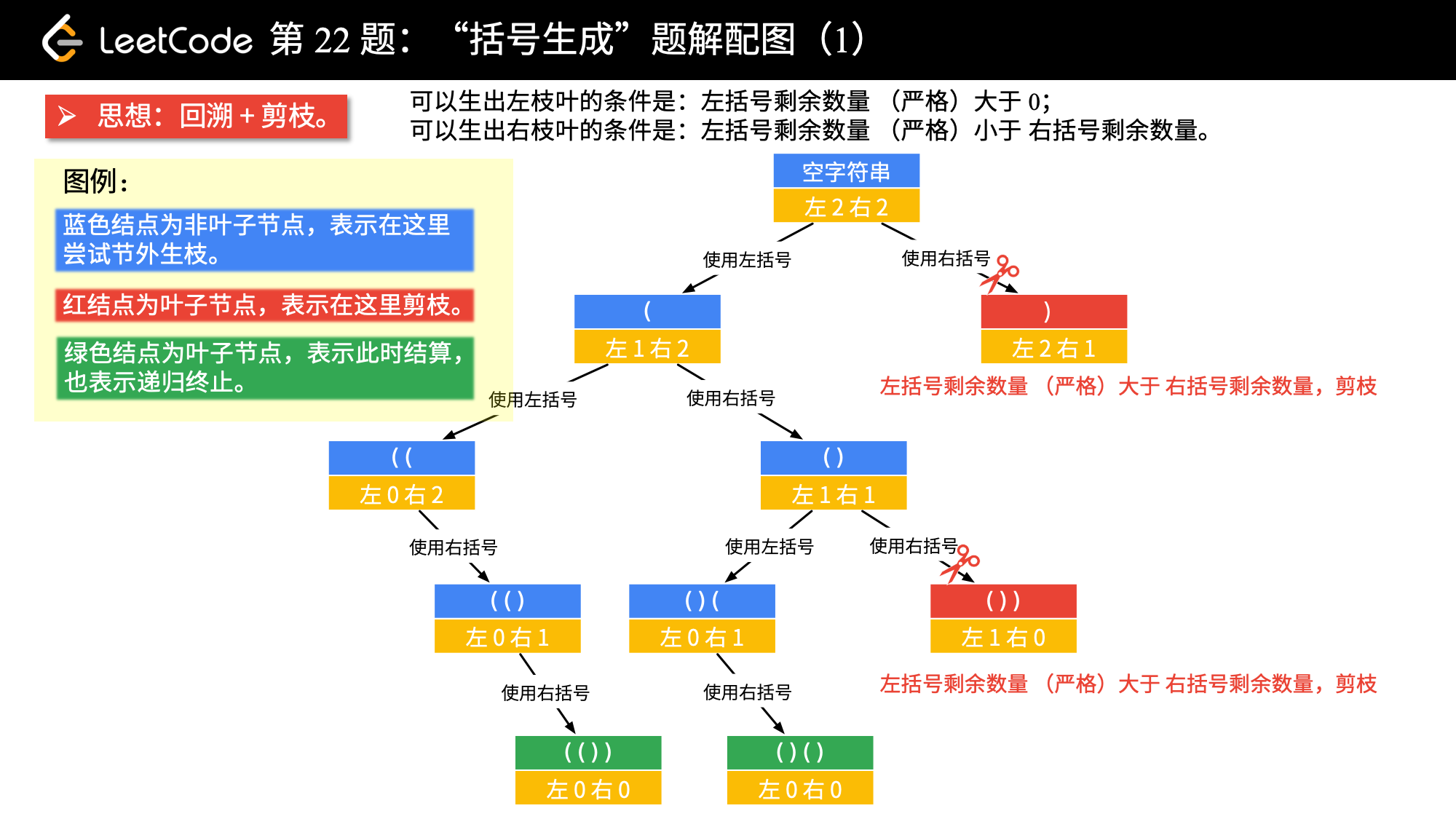{width=”90%” align=”center”}

这里主要使用了回溯方法实现DFS,首先安装括号类型分为两部分，当左和右都同时为0，说明到了最底下，此时添加到result中，
在程序中，我们可以看到这是一种减法操作，每次进入一层递归函数，就会减去1，直到最后为0。

但是回溯方法往往需要剪枝来减小时间复杂度，因此剪枝的条件：left > right。因为是按照从左向右依次添加括号，所以左边剩余的括号总是比右边剩余的括号小，除了叶子结点。

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        result = []
        cur_str = ''
        # dfs深度优先遍历
        def dfs(cur_str,left,right):
            if left == 0 and right == 0:
                result.append(cur_str)
                return
            if left > right:
                # 剪枝
                return
            #递归左子树
            if left > 0:
                dfs(cur_str+'(',left-1,right)
            #递归右子树
            if right > 0:
                dfs(cur_str+')',left,right-1)
        dfs(cur_str,n,n)
        return result

总结一下：

本题中dfs比dp的效率要高，原因在于回溯加了剪枝。在面对dfs或者bfs时候，最好能够数形结合。动态规划在于将问题分解为小问题进行求解。