手写感知机算法

一、背景

在阅读了李航的《统计学习方法》第2章后，对自己的学习做个笔记，手写一个感知机算法，练练手。

感知机是二分类的线性分类模型，对于每一个输入的样本，感知机的原始形式是一个关于w,b的超平面。
感知机的学习过程是通过对数据集进行训练，找出最优的参数w,b，形成对应的超平面，将数据集分为无误判的两类。
训练过程即求解最优参数的过程，构造基于误分类的函数间距的Loss Function，学习的目标是找到使损失函数极小化的w和b，优化算法采用梯度下降算法，不断迭代更新w和b，直至算法收敛。最终求解出感知机模型。

感知机算法分为原始形式和对偶形式。下面分别手写两种形式的算法。

注：本篇笔记侧重实现代码实现算法

二、原始形式和对偶形式算法实现

1.学习目标为w和b的感知机算法的原始形式

from typing import *
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
class Perception(object):
    # 感知机
    def __init__(self, 
                 n_features: int,
                 iter_counts: int,
                 n_samples: int,
                 category: int,
                 ):
        self.iter_counts = iter_counts  # 迭代次数
        self.n_samples = n_samples      # 样本数量
        self.learning_rate = 1  # 学习率
        self.n_features = n_features   # 样本特征维度
        self.category = category      # 分类类别
        self.w = 0            # 参数w
        self.b = 0            # 参数b
        self.x = None         # 训练集
        self.y = None         # 训练集对应的标签
        self.pot_size = 10    # 散点图中点大小
        self.errors = []      # 每次迭代中出现的误分类次数
        
    def generate_data(self):
        """
        数据生成
        """
        # 生成样本总容量为1500, 样本特征维度x(x1, x2)二维，分类类别两类，横纵轴边界在[-10, 10]范围内的数据集
        # centers:表示分类类别, n_features表示样本特征维度大小, center_box表示横纵轴边界范围
        my_data = datasets.make_blobs(n_samples=self.n_samples, 
                                      n_features=self.n_features,
                                      centers=self.category,
                                      center_box=(-10, 10)
                                      )
        self.x, self.y = my_data
        for idx, y in enumerate(self.y):
            if y == 0:
                self.y[idx] = -1
        # 绘制图像, c标识颜色, s表示大小
        # plt.scatter(self.x[:, 0], self.x[:, 1], c=self.y, s=self.pot_size)
    
    @staticmethod
    def cal_y(data: np.ndarray, w: np.ndarray, b: int):
        """
        计算wx + b
        """
        return np.dot(data, w) + b
    
    def generate_gram(self) -> List[List[float]]:
        """
        生成gram矩阵
        """
        # gram = [[0 for _ in range(self.n_samples)] for _ in range(self.n_samples)]
        # for i in range(self.n_samples):
        #     for j in range(i, self.n_samples):
        #         gram[j][i] = gram[i][j] = np.dot(self.x[i], self.x[j])

        z = np.transpose(self.x)
        gram = np.dot(self.x, z)
        return gram
        
    def train_origin(self) -> Tuple[np.ndarray, float]:
        """
        原始形式
        """
        # 训练模型
        self.errors = []
        w = np.random.rand(self.n_features, 1)
        b = 1
        i = 0
        while i < self.iter_counts:
            error = 0 # 记录误分的次数
            for j in range(self.n_samples):
                xj, yj = self.x[j], self.y[j]
                y_value = self.cal_y(xj, w, b)
                if yj * y_value <= 0:
                    error += 1
                    # 给xj纵上增加一个维度,使之为2行1列
                    # print(xj, yj)
                    w += self.learning_rate * np.expand_dims(xj, 1) * yj
                    b += self.learning_rate * yj
            self.errors.append(error)
            # 无错分停止迭代
            if error == 0:
                break
            i += 1
        
        if i == self.iter_counts:
            print(f"在{self.iter_counts}有限迭代次数中总存在误分类情况")
        self.w, self.b = w, b
        return w, b
    
    def train_dual(self) -> Tuple[np.ndarray, float]:
        """
        对偶形式
        """
        self.errors = []
        gram = self.generate_gram()
        a, b, i = np.zeros([self.n_samples, 1]), 0, 0
        while i < self.iter_counts:
            error = 0
            for j in range(self.n_samples):
                yj = self.y[j]
                # y_value = b
                y_value = np.dot(gram[j], a * np.expand_dims(self.y, 1)) + b
                # for k in range(self.n_samples):
                #     y_value += a[k] * self.y[k] * gram[j][k]
                if yj * y_value <= 0:
                    # 出现误分类
                    error += 1
                    a[j] += self.learning_rate
                    b += self.learning_rate * yj
            self.errors.append(error)
            if error == 0:
                break
            i += 1
        if i == self.iter_counts:
            print(f"在{self.iter_counts}有限迭代次数中总存在误分类情况")
        w = np.zeros([2, 1]).flatten()
        for j in range(self.n_samples):
            w += a[j] * self.y[j] * self.x[j]
        self.w, self.b = w, b
        return w, b
                
        
    
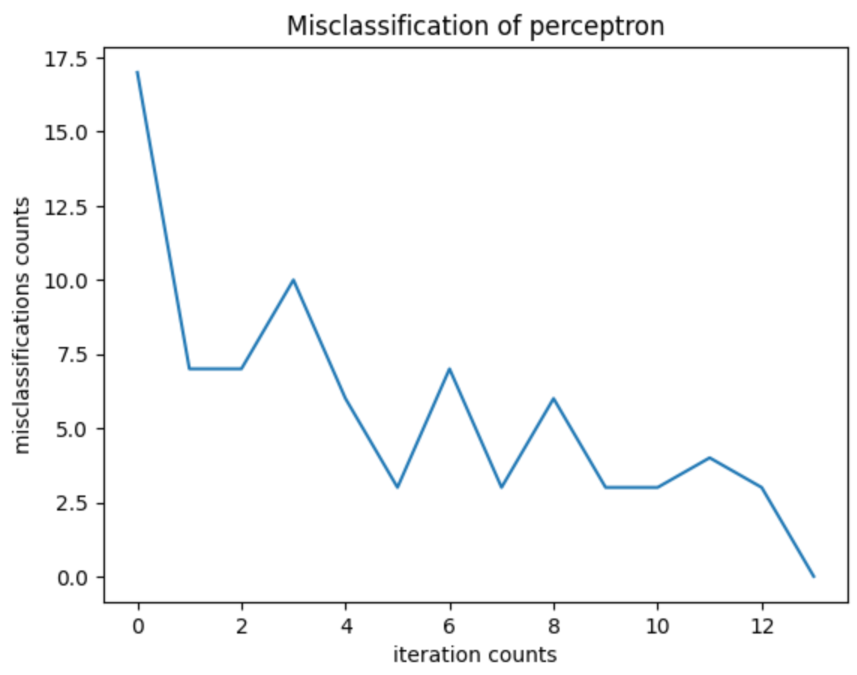
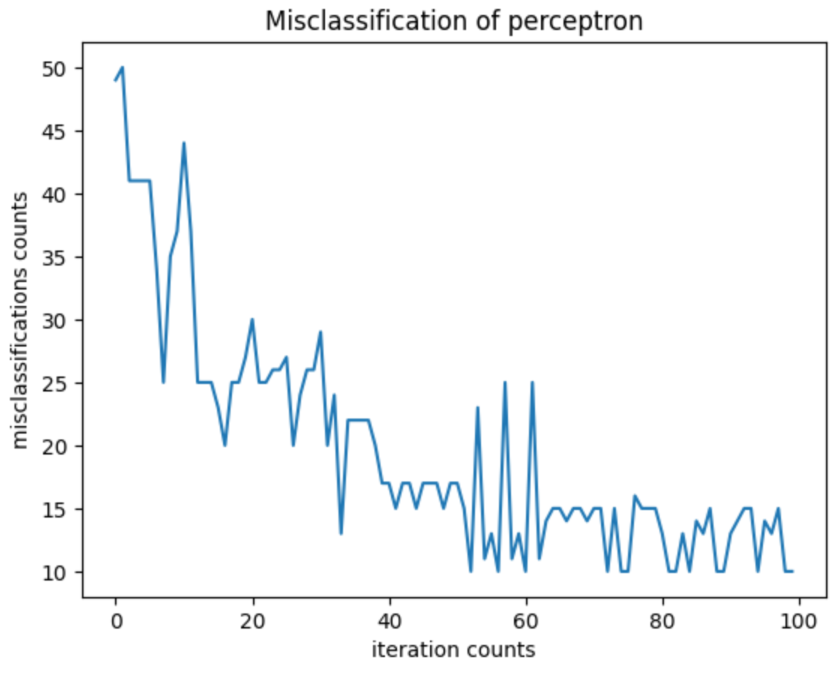
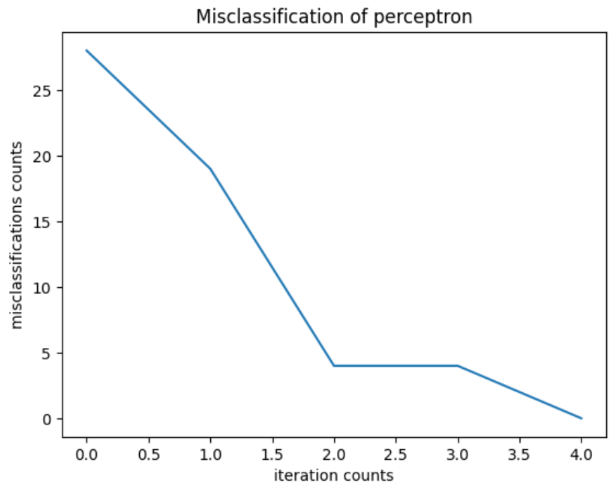
    def error_gui(self):
        """
        每次迭代的误分类次数---折线图
        """
        print(f"参数w: {self.w.flatten()}, b： {self.b}", )
        print("迭代次数：", self.iter_counts)
        fig = plt.figure()
        # 创建一行一列一个坐标区
        ax = fig.subplots(1,1)
        ax.set_title('Misclassification of perceptron')
        ax.set_xlabel('iteration counts')
        ax.set_ylabel('misclassifications counts')
        ax.plot(range(len(self.errors)), self.errors)
        plt.show()
        
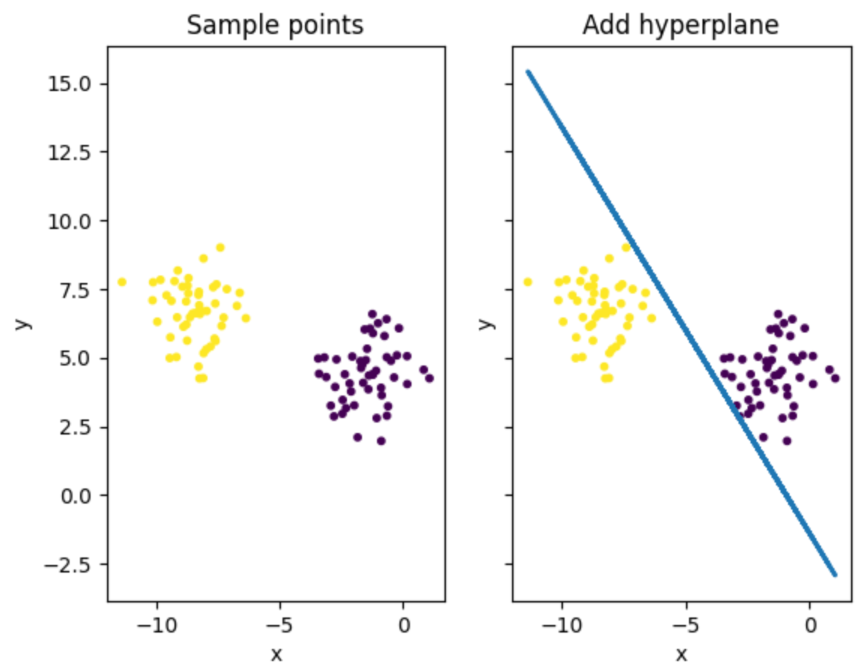
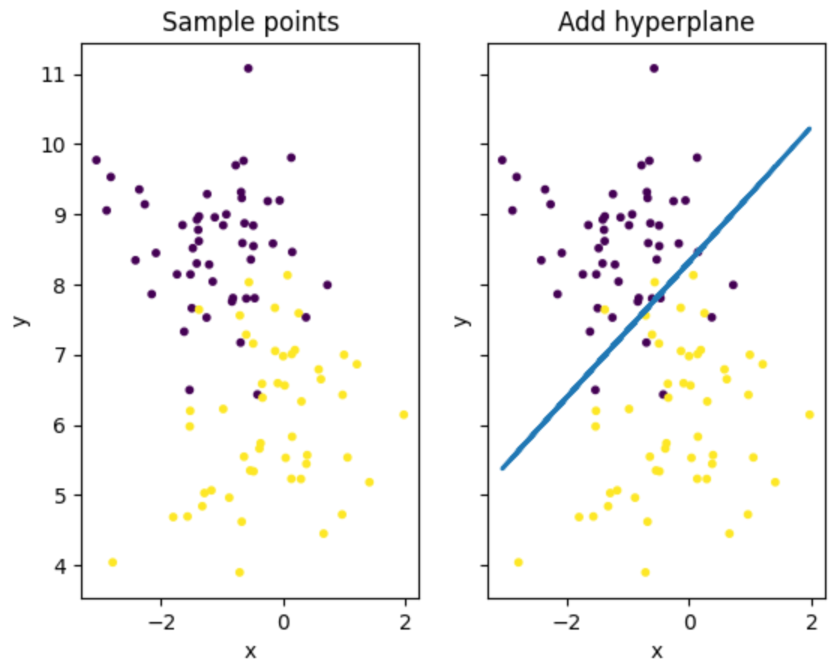
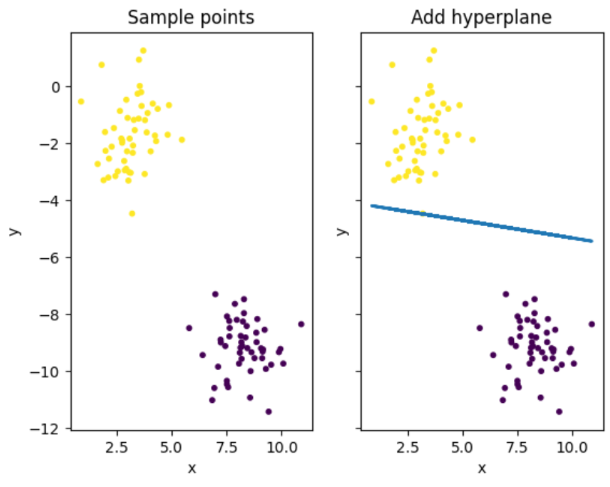
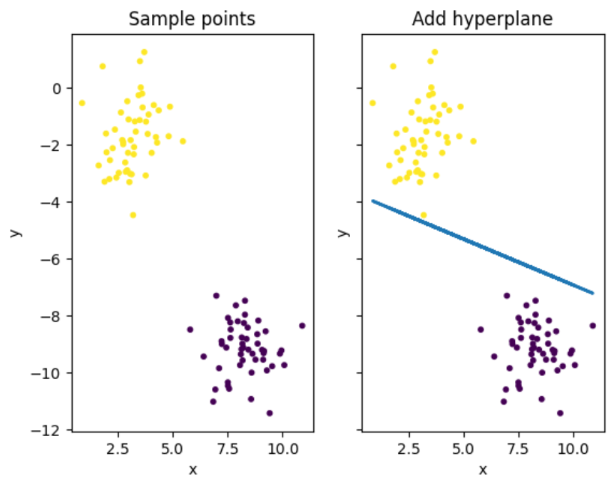
    def hyperplane_gui(self):
        """
        训练出来的超平面
        """
        fig = plt.figure()
        # 共享纵横轴
        ax1, ax2 = fig.subplots(1, 2, sharex=True, sharey=True)
        ax1.set_title('Sample points')
        ax1.set_xlabel('x')
        ax1.set_ylabel('y')
        ax1.scatter(self.x[:, 0], self.x[:, 1], c=self.y, s=self.pot_size)

        ax2.set_title('Add hyperplane')
        ax2.set_xlabel('x')
        ax2.set_ylabel('y')
        ax2.scatter(self.x[:, 0], self.x[:, 1], c=self.y, s=self.pot_size)
        ax2.plot(self.x[:, 0], (-self.b - self.x[:, 0] * self.w[0]) / self.w[1], linewidth=2.0)
        plt.show()
        
    def run(self, use_dual: bool = False) -> None:
        
        if use_dual:
            self.train_dual()
        else:
            self.train_origin()
        p.error_gui()
        p.hyperplane_gui()

1
2
3

p = Perception(2, 100, 100, 2)
p.generate_data()
p.run()

运行效果：

例1：对于线性可分数据集：

1
2
3

finish
参数w: [-32.54612901 -22.07273347], b： -30
迭代次数： 13

例2：对于线性不可分数据集：

在100有限迭代次数中总存在误分类情况
finish
参数w: [ 1.14560324 -0.82259786], b： -2
迭代次数： 100

1.学习目标为ni, i = 1,2,3,4,5….的感知机算法的对偶形式

只需要重写个train_dual算法，其余部分代码不需要动。

对偶形式，通过将w,b转换成关于ni（每个实例点的误分类次数）的增量，将学习目标转变成求解ni，即求损失函数极小值下的，求解最优参数ni。ni表示实例点更新的次数，即误分类次数，更新次数越多意味着实例点离超平面越近，对学习结果的影响越大。实现代码如下：

class Perception(object):
    
	def train_dual(self) -> Tuple[np.ndarray, float]:
        """
        对偶形式
        """
        gram = self.generate_gram()
        a, b, i = np.zeros([self.n_samples, 1]), 0, 0
        while i < self.iter_counts:
            error = 0
            for j in range(self.n_samples):
                yj = self.y[j]
                y_value = b
                # 更新ai
                for k in range(self.n_samples):
                    y_value += a[k] * self.y[k] * gram[j][k]
                if y_value * yj <= 0:
                    # 出现误分类
                    error += 1
                    a[j] += self.learning_rate
                    b += self.learning_rate * yj
            if error == 0:
                break
            i += 1
        if i == self.iter_counts:
            print(f"在{self.iter_counts}有限迭代次数中总存在误分类情况")
        w = np.zeros([2, 1]).flatten()
        for j in range(self.n_samples):
            w += a[j] * self.y[j] * self.x[j]
        self.w, self.b = w, b
        return w, b

p = Perception(2, 100, 100, 2)
p.generate_data()
print('采用原始形式训练')
p.run()
print('采用对偶形式训练')
p.run(True)

测试结果：

采用原始形式训练
参数w: [1.05789363 8.55426604], b： 35
迭代次数： 100
采用对偶形式训练
参数w: [2.52959839 7.83869324], b： 29
迭代次数： 100

原始形式：

对偶形式

三、总结

对于线性可分的数据集，如例1，感知机算法能够在有限的迭代次数内通过梯度下降算法找到最优参数，使得损失函数极小化，找到一个线性超平面去拟合所有实例点。
对于线性不可分的数据集，如例2，感知机算法无法收敛于最优参数解。
感知机算法主要用于二分类问题，其局限性很大，实际场景几乎不用。
对偶形式的感知机算法相对于原始形式来说，主要的区别在于，对偶形式下感知机算法学习的目标由对求w,b参数的最优解转变为求 ni的最优解, 通过将w,b转换为ni(每个实例点误分类的次数)。通过预计算Gram矩阵，将参数更新过程中涉及到的内积运算xi 和 xj的内积计算出来，当样本特征过高时，迭代更新变量时计算的内积非常耗时，因此通过预处理，然后直接查Gram矩阵表，可以加速模型训练速度，加速收敛。
通过最后4幅图，分别使用原始形式和对偶形式训练过程可以看出，对偶形式的迭代次数要比原始形式要少，因此符合其可以加速模型收敛速度的优势。

Python 机器学习人工智能

Python 机器学习感知机算法人工智能

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

详解Python types类型模块下一篇